Паралелограм

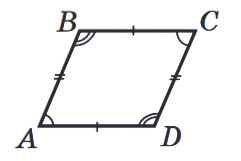
Паралелограм – це чотирикутник, у якого протилежні сторони попарно паралельні.

Типи паралелограмів:

Існує декілька типів паралелограмів, залежно від їхніх властивостей:

• Прямокутник: Паралелограм, у якого всі кути прямі.
• Квадрат: Паралелограм, у якого всі кути прямі і всі сторони рівні.
• Ромб: Паралелограм, у якого всі сторони рівні, але кути не прямі.

Властивості паралелограма

• Протилежні сторони рівні:

AB = CD, AD = BC.

• Протилежні сторони паралельні:

AB || CD, AD || BC.

• Протилежні кути рівні:

∠A = ∠C, ∠B = ∠D.

• Сума сусідніх кутів дорівнює 180°.

∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180°.

• Діагоналі паралелограма перетинаються та точкою перетину діляться навпіл.

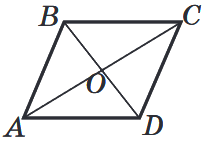
AO = OC, BO = OD.

• Діагональ ділить паралелограм на два рівних трикутника.

∆ABD = ∆CDB, ∆ABC = ∆CDA.

• Сума квадратів діагоналей дорівнює сумі квадратів чотирьох сторін.

AC² + BD² = 2AB² + 2AD²

• Діагоналі паралелограма поділяють його на чотири рівновеликі трикутники.

S_{∆ AOB} = S_{∆ BOC} = S_{∆ COD} = S_{∆ AOD}

Периметр паралелограма

Периметр паралелограма – це сума довжин всіх його сторін.

Оскільки протилежні сторони паралелограма рівні, для його знаходження можна використовувати наступну формулу:

P = 2a + 2b,

де:

• P – периметр паралелограма;
• a – довжина однієї сторони паралелограма;
• b – довжина іншої сторони паралелограма.

Наприклад:

Дано паралелограм зі сторонами 5 см і 7 см.

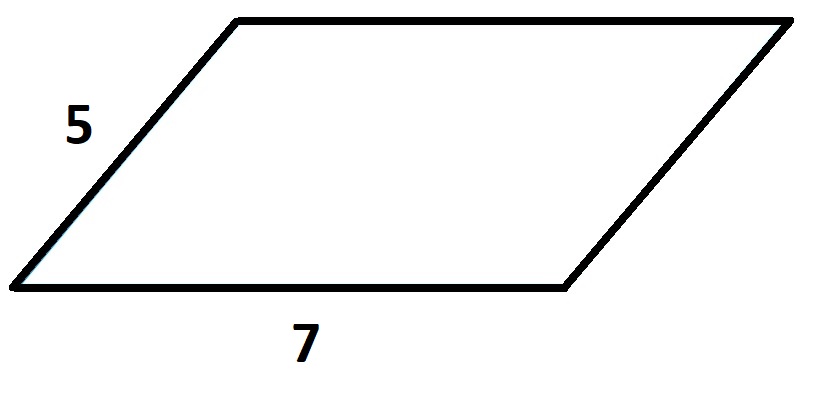
Обчислимо його периметр:

P = 2 ∙ 5 см + 2 ∙ 7 см = 10 см + 14 см = 24 см.

Таким чином, периметр даного паралелограма дорівнює 24 см.

Площа паралелограма

Площа паралелограма дорівнює добутку довжини його основи на довжину висоти, проведеної до цієї основи.

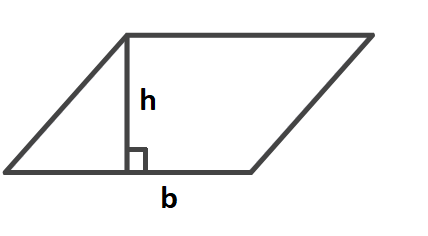
Формула:

S = b ∙ h,

де:

• S – площа паралелограма;
• b – довжина основи паралелограма;
• h – довжина висоти, проведеної до цієї основи.

Основою паралелограма може бути будь-яка з його сторін.

Висота – це перпендикуляр, проведений з будь-якої вершини паралелограма до протилежної сторони (основи).

Наприклад:

Дано паралелограм зі сторонами 6 см і 4 см. Висота, дорівнює 5 см.

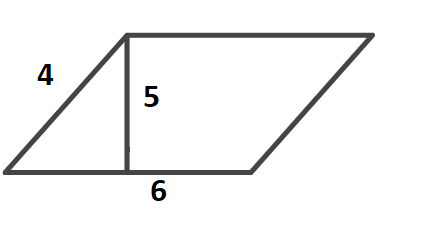
Обчислимо площу паралелограма:

S = 6 см ∙ 5 см = 30 см².