Діагональ – це пряма лінія, яка з’єднує дві протилежні вершини в прямокутнику, площинній фігурі або паралелограмі, які не належать одній грані.
Властивості діагоналі
Основні властивості діагоналі залежать від типу фігури, в якій вона використовується.
Основні властивості діагоналей для різних геометричних фігур:
Діагональ прямокутника
- Діагональ в прямокутнику ділять його на два рівні прямокутні трикутники.
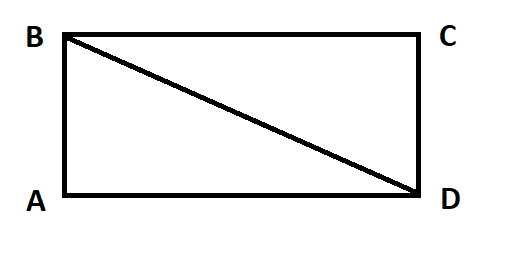
- За теоремою Піфагора, довжина діагоналі (d) прямокутника зі сторонами a та b задається формулою: d = √(a2 + b2).
- Дві діагоналі прямокутника мають однакову довжину.
Діагоналі квадрата
- У квадраті діагоналі є рівні та перпендикулярні одна одній.
- Діагоналі квадрата є бісектрисами його кутів
- Знаходження довжини діагоналі квадрата: d = a√2, де a – довжина сторони квадрата.
- Діагоналі квадрата ділять його на чотири рівні рівнобедрені трикутники
Діагональ паралелограма
- Діагоналі паралелограма розділяють його на два рівні трикутники.
- Сума квадратів довжин діагоналей паралелограма дорівнює сумі квадратів довжин всіх його сторін.
Діагональ трапеції
- Діагоналі трапеції не є рівними, але вони розділяють її на два рівні трикутники.
- Довжина діагоналі трапеції може бути знайдена за допомогою піфагорової теореми, використовуючи довжини бічних сторін і висоти.
Діагоналі багатокутників
- У багатокутнику діагоналі – це лінії, які з’єднують неконсективні вершини (вершини, які не є сусідніми).
- Кількість діагоналей в багатокутнику з n вершинами може бути знайдена за формулою: N = n(n-3)/2.


