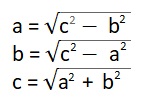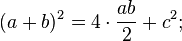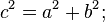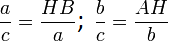Теорема Піфагора – це одна з основних теорем евклідової геометрії, яка встановлює співвідношення між сторонами прямокутного трикутника.
Теорема Піфагора
Теорема Піфагора звучить так:
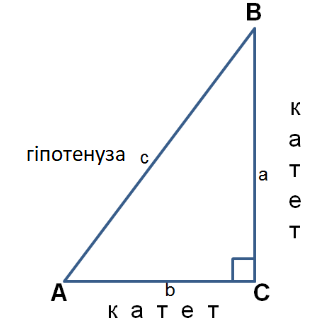
У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи.
Це означає, що якщо у нас є прямокутний трикутник з катетами a та b і гіпотенузою c, то a² + b² = c².
a, b — катети, с — гіпотенуза.
З цієї формули можна вивести наступне:
Алгебраїчне доведення теореми Піфагора
Один з алгебраїчних способів доказу теореми Піфагора полягає у використанні площ фігур. Цей метод полягає у розташуванні однакових прямокутних трикутників таким чином, щоб всередині утворився квадрат. Кожна сторона зовнішнього квадрата повинна складатися з суми катетів прямокутного трикутника a + b.
Площу цього квадрата можна буде знайти завдяки формулі:
Внутрiшнiй чотирикутник можна вважати квадратом, адже, якщо додати два гострі кути прямокутного трикутника, то вийде 90°. Слід вважати, що площа зовнішнього квадрата складається з площi внутрiшнього квадрата і чотирьох площ однакових прямокутних трикутників.
Це доводить теорему Піфагора.
Доведення теореми Піфагора за подібністю трикутників
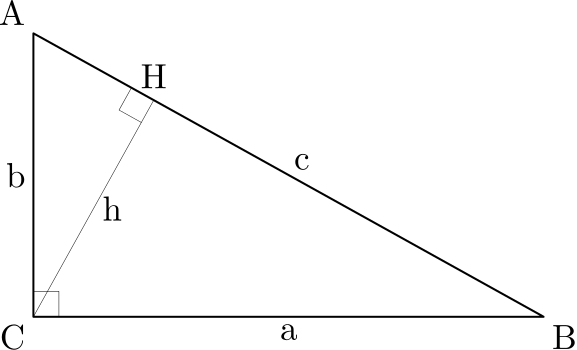
Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C, і назвемо H точку перетину з стороною AB. Утворений трикутник ACH подібний до трикутника ABC, оскільки вони обидва прямокутні (за визначенням висоти), і в них спільний кут A, очевидно третій кут буде в цих трикутників також однаковий. Аналогічно міркуючи, трикутник CBH також подібний до трикутника ABC.
З подібності трикутників:
Якщо
тоді
Це можна записати у вигляді
Якщо додати ці дві рівності, отримаєм
Іншими словами, Теорема Піфагора:
Історія теореми Піфагора
Мегалітичні споруди близько 2500 до н. е. в Єгипті та Північній Європі містять прямокутні трикутники зі сторонами з цілих чисел. Бартель ван дер Варден висловив гіпотезу, що в ті часи Піфагорові числа були знайдені алгебраїчно.
Написаний між 2000 та 1876 до н. е. папірус часів Середнього Єгипетського царства Berlin 6619 містить задачу, розв’язком якої є числа Піфагора. Написана під час правління Хамурапі Великого (між 1790 і 1750 до н.е) вавилонська табличка Plimpton 322 містить багато записів, тісно пов’язаних з числами Піфагора. У сутрах Будхаяни, які датуються за різними версіями 8-им чи 2-им століттям до н. е. в Індии, містяться Піфагорові числа, віведенніе алгебраїчно, формулювання теореми Піфагора і геометричний доказ для рівснобедреного прямокутного трикутника.
Історія теореми Піфагора стверджує, що перший доказ не належить Піфагору. Цілком імовірно, що зовсім не він довів теорему, яка тим не менш носить його ім’я.
Піфагор Самоський був давньогрецьким математиком, філософом і містиком. Він народився в 570 році до н. е. на острові Самос і був названий «найбільшим еллінським мудрецем». Піфагор заснував релігійно-філософську школу піфагореїзму, яка стала легендою і джерелом дискусій уже в стародавні часи.
Завстосування теореми Піфагора
Теорема Піфагора має багато застосувань у математиці та повсякденному житті.
Ось декілька прикладів:
- Вона використовується для розрахунку відстаней у дво- та тривимірних просторах. Наприклад, вона може бути використана для розрахунку відстані між двома точками на карті або для розрахунку довжини діагоналі прямокутника.
- Вона також може бути використана для розрахунку висоти об’єктів. Наприклад, якщо у нас є лазерний дальномір, ми можемо виміряти відстань до підніжжя дерева та кут між лазером та землею. З цих даних ми можемо розрахувати висоту дерева за допомогою теореми Піфагора.
- Вона також може бути використана у будівництві для перевірки прямокутності кутів. Наприклад, якщо ми хочемо перевірити, чи є кут між двома стінами прямим, ми можемо заміряти довжини трьох сторін прямокутного трикутника, утвореного цими стінами та підлогою. Якщо сума квадратів катетів дорівнює квадрату гіпотенузи, то кут є прямим.
Це лише декілька прикладів застосування теореми Піфагора. Ця теорема є одним з найбазовіших інструментів у математиці та науці і має безліч застосувань.