Трикутники

Трикутники – це геометричні фігури, які складаються з трьох сторін та трьох кутів.

Трикутник складається з трьох точок, які називаються вершинами, і трьох відрізків, які називаються сторонами.
Кожен кут трикутника утворюється зі з’єднання двох сторін і має величину, вимірювану в градусах.

Трикутник є базовою фігурою в геометрії і він може бути різних видів, залежно від довжин сторін та величин кутів.

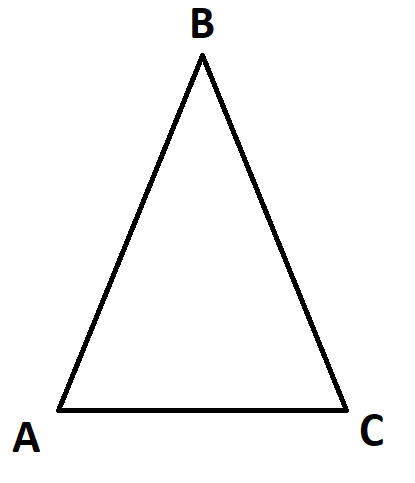
Трикутник із вершинами А, В, С і сторонами АВ, ВС, АС.

Цей трикутник позначається так: ∆ АBC

∠A — позначають однією буквою, що вказує його вершину (наприклад, «кут A трикутника ABC»).

Види трикутників

Трикутники можна класифікувати за довжиною сторін та величиною кутів.

За довжиною сторін:

Різносторонній трикутник

Різносторонній трикутник – це трикутник, у якого всі три сторони мають різні довжини. Це означає, що жодні дві сторони не можуть мати однакову довжину.

У різносторонньому трикутнику всі три кути також мають різні величини. Кути можуть бути гострокутними (менше 90 градусів), тупокутними (більше 90 градусів) або прямими (90 градусів).

Різносторонній трикутник є найбільш загальним типом трикутника і може мати різні форми та пропорції. Його властивості та характеристики можуть варіюватися в залежності від конкретних довжин сторін і величин кутів.

Для різностороннього трикутника не існує специфічних співвідношень між сторонами та кутами, які були б унікальними для цього типу трикутника. Властивості різностороннього трикутника можуть бути застосовані до будь-якого трикутника, у якому сторони мають різні довжини.

Периметр різностороннього трикутника

Периметр різностороннього трикутника обчислюється шляхом додавання довжин усіх його сторін. Якщо позначити сторони трикутника як a, b і c, то формула для обчислення периметру (P) буде такою:

P = a + b + c

Де a, b і c – довжини різних сторін трикутника.

Площа різностороннього трикутника

Площа різностороннього трикутника може бути обчислена за допомогою формули Герона, яка використовує довжини сторін трикутника. Нехай a, b і c – довжини сторін, а s – півпериметр (півсума довжин сторін):

s = (a + b + c) / 2

Тоді площа (A) різностороннього трикутника може бути обчислена за формулою:

Рівнобедрений трикутник

Рівнобедрений трикутник – це трикутник, що має дві рівні сторони та два рівні кути біля цих сторін. Третій кут рівнобедреного трикутника завжди менший за два однакових кути.

Основні характеристики рівнобедреного трикутника:

• Дві сторони, що мають однакову довжину, називаються рівнобічними сторонами.
• Довжина третьої сторони називається основою.
• Висота рівнобедреного трикутника є перпендикуляром, спущеним з вершини основи до протилежної сторони. Вона також є медіаною і бісектрисою відповідного кута.
• Медіана рівнобедреного трикутника – це відрізок, що з’єднує середини основи і вершини кута. У рівнобедреному трикутнику медіана також є висотою і бісектрисою відповідного кута

Периметр рівнобедреного трикутника

P = 2a + b

де a – довжина рівнобічної сторони, b – довжина основи.

Площа рівнобедреного трикутника

a – довжина рівнобічної сторони, b – довжина основи.

Рівносторонній трикутник

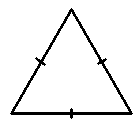
Рівносторонній трикутник – це трикутник, у якого всі три сторони мають однакову довжину, а всі три кути мають однакову міру, рівну 60 градусам. Іншими словами, всі сторони і всі кути рівностороннього трикутника є однаковими.

Основні характеристики рівностороннього трикутника:

• Усі сторони рівностороннього трикутника мають однакову довжину.
• Усі кути рівностороннього трикутника дорівнюють 60 градусам.
• Усі медіани, висоти і бісектриси рівностороннього трикутника збігаються у точці перетину центральних перпендикулярів (центр вписаного кола) трикутника.
• Усі бісектриси, медіани і висоти рівностороннього трикутника збігаються у точці перетину централізованих кіл (центр описаного кола) трикутника.

Периметр рівностороннього трикутника

Периметр рівностороннього трикутника можна обчислити, враховуючи те, що всі його сторони мають однакову довжину. Якщо позначити довжину сторони рівностороннього трикутника як “a”, то периметр (P) визначається так:

P = 3a

Тобто периметр дорівнює трьом довжинам сторони, оскільки всі вони є однаковими.

Площа рівностороннього трикутника

а – довжина сторони.

За величиною кутів:

Гострокутний трикутник

Гострокутний трикутник – це трикутник, у якому всі три кути є гострими кутами, тобто кожен кут менший за 90 градусів.

Гострокутний трикутник має деякі властивості:

1. У гострокутному трикутнику найбільша сторона лежить навпроти найбільшого кута, а найменша сторона – навпроти найменшого кута.
2. Гострокутний трикутник може бути рівнобедреним (з двома однаковими сторонами) або рівностороннім (зі всіма сторонами однакової довжини).
3. У гострокутному трикутнику виконується теорема синусів та теорема косинусів, які дозволяють обчислити довжини сторін та величини кутів за відомими даними.

Тупокутний трикутник

Тупокутний трикутник: має один тупий кут (кут більше 90 градусів).

Тупокутним трикутником буде називатися будь-який трикутник, що містить тупий кут.

Тупокутний трикутник може бути рівнобедреним, але при цьому не може бути рівностороннім або прямокутним.

Прямокутний трикутник

Прямокутний трикутник – це трикутник який має один прямий кут (кут рівний 90 градусів).

У прямокутному трикутнику сторона, яка лежить навпроти прямого кута, називається “гіпотенузою”, а дві інші сторони називаються “катетами”.

Деякі властивості прямокутних трикутників:

• Гіпотенуза – це найдовша сторона прямокутного трикутника, яка знаходиться проти прямого кута.
• Катет – це будь-яка зі сторін прямокутного трикутника, яка прилягає до прямого кута.
• Теорема Піфагора стверджує, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його катетів: a² + b² = c².
• Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то катет протилежній цьому куту буде дорівнювати половині гіпотенузі.
• Точка перетину бісектрис двох гострих кутів прямокутного трикутника лежить на гіпотенузі і ділить її на дві рівні частини.
• Прямокутний трикутник можна поділити на два менші прямокутні трикутники, використовуючи висоту, проведену до гіпотенузи.
• Всі висоти трикутника перетинаються в одній точці – ортоцентрі.

Площу прямокутного трикутника можна обчислити за формулою:

A = (1/2) ∙ a ∙ b

де A – площа, а і b – довжини катетів.

Ознаки рівності трикутників

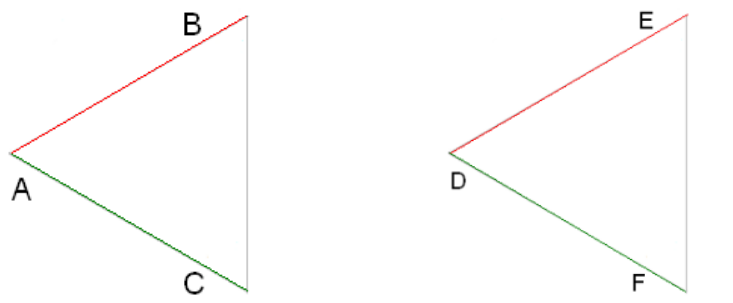
• Перша ознака

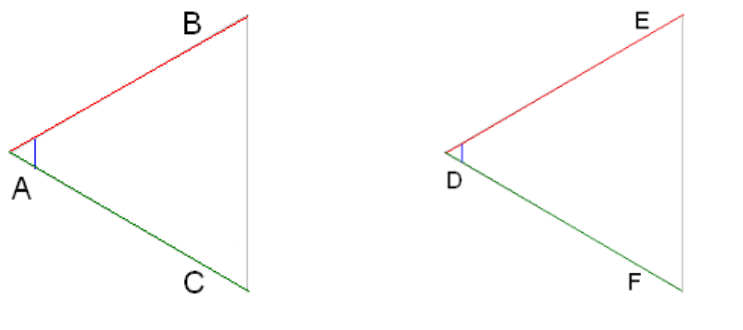
Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам та куту між ними іншого трикутника, то такі трикутники рівні.

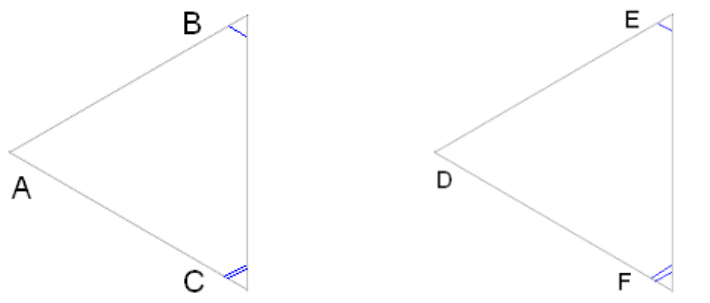
• Друга ознака

Якщо сторона і два прилеглих до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.

• Третя ознака

Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.

Ознаки подібності трикутників

Є кілька ознак, які дозволяють встановити подібність двох трикутників:

• Кути: якщо два трикутники мають однакові кути, то вони подібні. Це називається “кутовою ознакою подібності трикутників”. Це означає, що відповідні кути у цих трикутників мають однакові величини.
  
  

• Сторони: якщо відношення довжин сторін двох трикутників є рівними, то вони подібні. Це називається “сторонньою ознакою подібності трикутників”. Це означає, що відповідні сторони у цих трикутників мають пропорційні довжини.
  
  

• Кут і сторона: якщо у двох трикутників один кут має однакову величину, а відповідні сторони відносяться між собою у рівних пропорціях, то ці трикутники є подібними. Це називається “кутово-сторонньою ознакою подібності трикутників”.

Зауважимо, що подібність трикутників зберігається під час збільшення або зменшення їх розмірів, а також при повороті.

Висота трикутника

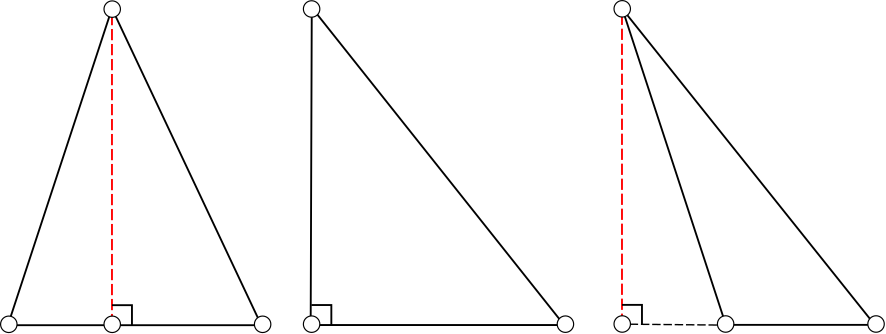
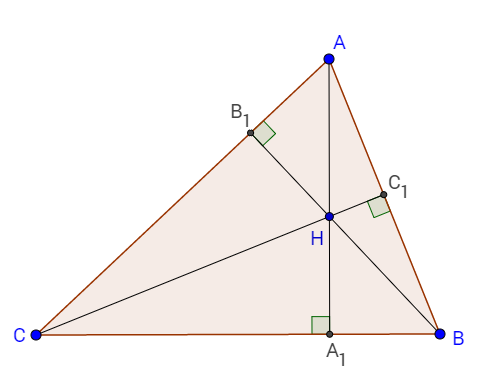
Висота трикутника – це перпендикуляр, проведений з вершини трикутника до протилежної сторони або до продовження протилежної сторони.
Висота може лежати в середині трикутника, на стороні або зовні трикутника.

Точку перетину висот трикутника називають ортоцентром.

В тупокутному трикутнику ортоцентр лежить поза межами трикутника.
В гострокутному — всередині трикутника.
В прямокутному трикутнику збігається з вершиною прямого кута.

Бісектриса трикутника

Бісектриса – це лінія, яка ділить внутрішній кут трикутника на два рівні кути. Таким чином, бісектриса ділить внутрішній кут трикутника на дві частини, які мають однакові величини.

В трикутнику можна провести три бісектриси – від кожної вершини до протилежної сторони. Місце перетину двох бісектрис називається центром вписаного кола трикутника, яке проходить через всі три сторони трикутника.

Медіана трикутника

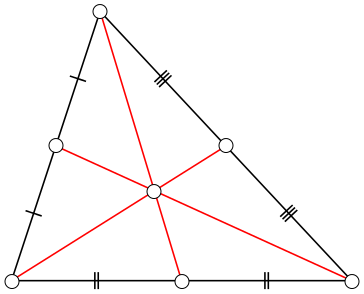
Медіана трикутника – це лінія, яка з’єднує вершину трикутника з серединою протилежної сторони, вона ділить трикутник на два трикутники однакової площі.
Три медіани перетинаються в одній точці, яка називається центроїдом трикутника. Ця точка є також центром мас трикутника.