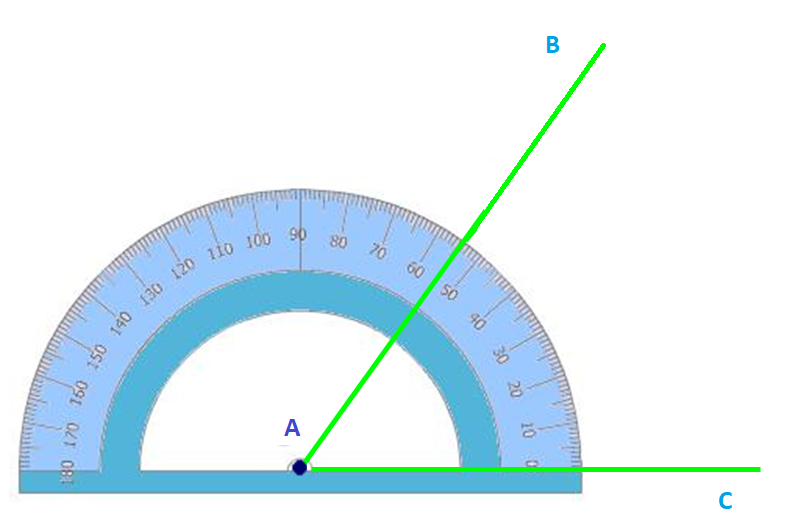
Кут – це фігура, утворена двома променями, які виходять з однієї точки.
Замість слова “кут” використовують знак 


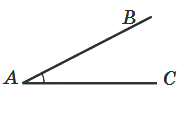
Будь‑який кут ділить площину на дві частини. Одну із частин називають внутрішньою областю кута, а іншу — зовнішньою.
- Внутрішня область кута – це частина площини, яка знаходиться всередині самого кута.
- Зовнішня область кута – це частина площини, яка не входить в сам кут, але знаходиться за межами його.
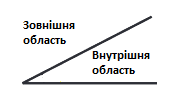
Основні елементи кута:
- Вершина кута: точка, з якої виходять сторони кута.
- Сторони кута: два промені, які утворюють кут.
- Величина кута: міра розвороту між сторонами кута. Виміряється в градусах (°) або радіанах. Величина кута показує, наскільки далеко один промінь повернувся відносно іншого.
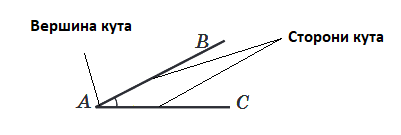
Сторонами кута будуть промені АВ і АС, вершиною точка А.
Види кутів
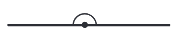
Розгорнутий кут
Розгорнутий кут – це кут, сторони якого лежать на одній прямій.
Має градусну міру 180∘
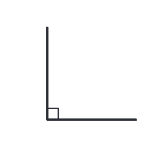
Прямий кут
Прямий кут – це кут, який дорівнює половині розгорнутого кута.
Має градусну міру 90∘ і утворюється двома перпендикулярними прямими.
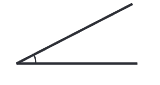
Гострий кут
Гострий кут – це кут, який менше прямого.
Має градусну міру менше 90∘.
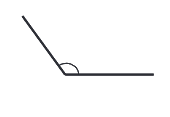
Тупий кут
Тупий кут – це кут, який більше прямого, але менше ніж розгорнутий.
Має градусну міру більше 90∘ , але менше 180∘.
Бісектриса кута
Бісектриса – це промінь, який виходить з вершини кута і ділить його навпіл.
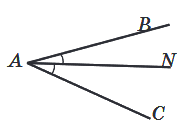
AN – бісектриса.
Рівні кути – це кути, які збігаються при накладенні. ∠BAN = ∠CAN
Суміжні та вертикальні кути
Суміжні кути
Суміжні кути – два кути, у яких одна сторона загальна, а дві інші є додатковими променями.
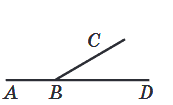
∠АВС та ∠CBD – суміжні кути.
Властивості суміжних кутів:
- Сума суміжних кутів дорівнює 180 °
- Якщо один з суміжних кутів прямий, то другий кут також прямий
- Якщо один з суміжних кутів гострий, то другий кут тупий.
- Якщо один з суміжних кутів тупий, то другий кут гострий.
- Бісектриси суміжних кутів утворюють прямий кут
- Якщо суміжні кути рівні, то вони прямі
- Якщо два кути рівні, то суміжні з ними кути також рівні.
- Два суміжних кути утворюють розгорнутий кут.
Вертикальні кути
Вертикальні кути – це два кути, сторони одного з яких є додатковими променями сторін іншого.
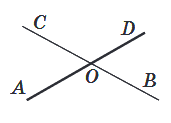
∠АОВ та ∠COD — вертикальні кути,
∠СОА та ∠DOB — вертикальні кути.
Властивості вертикальніх кутів
- Вертикальні кути рівні.
- Бісектриси вертикальних кутів утворюють розгорнутий кут.
Центральний та вписаний кути
Центральний кут
Центральний кут в колі – плоский кут з вершиною в її центрі.
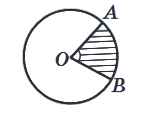
∠АОВ – центральний
Вписаний кут
Вписаний кут – це кут, вершина якого лежить на колі, а сторони перетинають це коло.
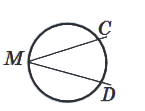
∠CMD – вписаний кут
Вимірювання кутів. Кутова міра.
Кутова міра
Одиниці вимірювання кутів у SI – це радіан. Має позначення рад (міжнародне — rad)
Один радіан — це площинний кут, утворений двома радіусами, так, що довжина дуги між ними дорівнює радіусу кола.
Але традиційно кути вимірюють у кути вимірюють у кутових градусах, мінутах і секундах. (позасистемна одиниця). Кожен із градусів ділиться на 60 мінут, кожна з мінут на 60 секунд.
Градуси позначаються значком °
Градус – це 1/360 частина повного оберта кола.
Розмір кута може бути виражений в будь-якій з цих одиниць виміру.
Існує просте співвідношення між градусами та радіанами:
- 1 радіан = 180° / π, тобто 1 Радіан = 57.2958 Градусів
- 1° = π / 180 радіанів, 1 Градус = 0.017453 Радіан.
Вимірювання кутів
Прилади для вимірювання кутів називаються кутомірами. Найпопулярніший із них транспортир. Використовувати як для вимірювання, так і для побудови кута певної величини.
Транспортир – це креслярський інструмент, що має форму півкола, поділеного на 180°, з лінійкою; за його допомогою будують і вимірюють кути на кресленнях. На ньому нанесені градусні поділки від 0 до 180 °, а у деяких моделях — від 0 до 360 °