Magnetic flux – is the flow of the magnetic induction vector through a certain surface. (symbol Φ)
In the SI system, the unit of magnetic flux is the weber (1 Wb = 1 V·s = 1 T·m² = 1 J/A = 108 maxwells in the CGS system – maxwell (1 Mx = 1 Gs·cm² = 10-8 Wb).
In a uniform magnetic field with a vector induction magnitude of B, a flat closed contour with an area S is placed. The normal n to the contour plane forms an angle α with the direction of the magnetic induction vector B.
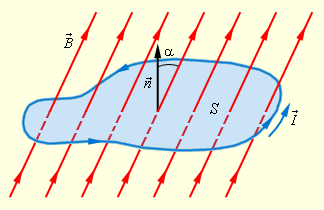
Magnetic flux is defined by the following relationship:
Φ = B · S · cos α
The magnetic flux through the contour is maximum when the contour plane is perpendicular to the magnetic field. Thus, the angle α is 0°. In this case, the magnetic flux is calculated using the following formula:
Φmax = B · S
The magnetic flux through the contour is zero when the contour is parallel to the magnetic field. In this case, the angle α is 90°.
Surfaces bounded by multiple contours
Frequently, situations arise when the lines of magnetic field induction intersect surfaces bounded by not one but several contours. For example, magnetic field lines may intersect surfaces bounded by coils of a solenoid that are parallel to each other and have the same surface area. In this case, the magnetic flux is determined by the formula:
Φ = NBS,
where:
N – the number of turns of the solenoid;
S – the surface area bounded by each turn.
Any changes in the magnetic field induction or the contour area result in changes in the magnetic flux, leading to the phenomenon of electromagnetic induction. Therefore, any change in magnetic flux results in the appearance of an electromotive force (EMF) in a closed conducting circuit. Taking into account Ohm’s law for a closed circuit, this conclusion can be expressed as follows: any change in magnetic flux leads to the occurrence of electromagnetic induction.