The Law of Universal Gravitation is a physical law that describes gravitational interaction within the framework of Newtonian mechanics.
It was formulated by the English physicist and mathematician Isaac Newton in 1687 in his work “Mathematical Principles of Natural Philosophy” (Philosophiæ Naturalis Principia Mathematica). This law describes the force of gravity between objects with masses and determines how this force depends on the masses of the objects and the distance between them.
Formulation of the law
The Law of Universal Gravitation is formulated as follows:
Every object in space attracts every other object with a force proportional to the masses of these objects and inversely proportional to the square of the distance between them.
Mathematically, this law is expressed as follows:
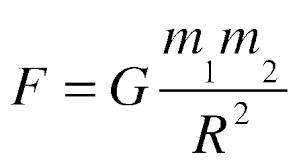

F – the force of gravity between objects
G – the gravitational constant (Newton’s constant)

m1 and m2 – the masses of the two interacting objects
R – the distance between the centers of mass of these objects.
The law of universal gravitation provides an accurate result when
- The sizes of the bodies are negligibly small compared to the distance between them, meaning that the bodies can be considered point masses.
- Both bodies have a spherical shape and a spherically symmetric distribution of matter. In this case, the distance between the bodies is taken as the distance between the centers of the spheres.
- One of the interacting bodies is a sphere with significantly larger dimensions and mass compared to the size and mass of the other body, which is located on or near the surface of this sphere.
Conclusion
This law served as the foundation for understanding gravitation and was a key achievement of Newton in the development of classical mechanics. It explains the motion of planets around the Sun, the falling of objects on Earth, and a wide range of other astronomical and physical phenomena in the universe.